これは
サイコロ
何回も振ればいずれの目も1/6で出現することになる
ということです。
確率が確率である以上
確率が収束するのは極めて当然のことです。
収束しない確率があるとすれば
インチキ。
イカサマ。
パチスロ。
・
・
・
パチスロにおいても
確率が収束するという前提は揺るぎません。
たしかに
パチスロは機械内部の抽選であり
サイコロのように物理的な動静を伴うものではないので
疑問も残る所ですが
一応
加盟団体の検査を受けていることからすれば
抽選方式に不正はないと見てよいでしょう
パチスロにおいても確率は収束するのです。
但し、これは何万回の試行の末の話であることに注意してください。
収束に必要な回数を求める公式があったと思うのですが
と思って捜した所
こちら
(東京大学大学院新領域創成科学研究科教授・
総合文化研究科及経済学研究科教授(兼)、
放送大学客員教授 松原 望教授のページ)
・
・
・
1%も理解できませんでした
いっぱいまわせば収束するということで^^;
確率統計学
ではなく
パチスロ確率論
として述べさせていただきます。
「確率は収束する」
という命題から
思いつくこと
それは
「確率は収束に向かうから、ハマリ台を狙え」
ちょっとばかし弁の立つ方が得意げに話しているのを耳にします。
そうなんですか?
おかしくないですか?
とすると
多少ハマったとしても
それは全体から見たら非常に小さい出来事です。
下の図で言うと
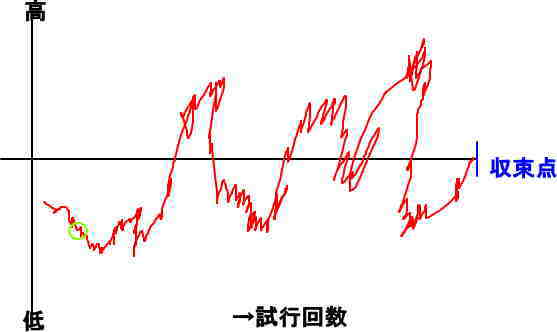
これを見ていただければ分かるように
たかだか何百、何千のゲーム数で確率が収束に向かうというのは
いかにも
視野が狭い論理といえます
この見解
(誰かが声高らかに主張しているわけではないと思いますが)
もしかしてA氏が・・・?(オカルト参照)
の最大の弱点というか欠陥について
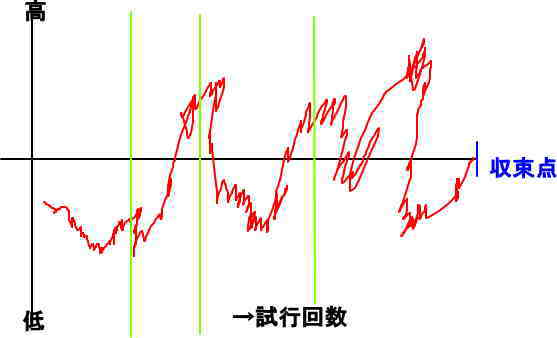
抽選は常に同じ確率で為されているわけです。
下の図でいうと緑線のどこにおいても同じ確率ですね。
前後の事情は全く関係しないはずです。
すなわち
緑線のいずれからはじまっても、やはり同じ確率です。
とすると
前の事情が後に影響するということを前提とするこの見解はNoです。
私は生じました。
前の事情が関係ないなら確率は収束しないのでは?
(例)
1/280で抽選
↓
10万回転の試行すべてで400回転目で当たる
確率は1/400で1/280でないじゃないか!
極端ながら例のようなことも考えられなくもないですよね。
実は
確率が収束するというのは結果論なんですね
1/Xで抽選を重ねた結果、トータルでは1/Xに近くなる。
初心にかえって
それぞれの目が1/6で出ることに疑問は生じませんね。
30回振って6が一回も出ないときにも
次に6が出る確率はやっぱり1/6ですね。
確率変動はしないです。
でも
何回も試行を重ねると6は1/6で出ますね。
このことが
パチスロでは
分母が大きくなる
演出が入る
金が絡む
等により
捻じ曲がってしまうのですね
の結論としましては
確率の収束とは、
その確率で抽選しているということ
それ以下でもそれ以上の意味もない
つまり
単なるトートロジー(循環論法)に過ぎないのですね
今後収束が云々言っている人を見かけたら
なま温かい目で見守ってあげましょう
| 関連事項 |
| TS式期待値講座 TS式本当に絶対勝てる講座 高設定台で勝つ 低設定台でも勝つ TS式確率の収束 |